Definitions
In aerodynamics, the lift-to-drag ratio is the amount of lift generated by a wing, compared to the drag it creates by moving through the air.
Thrust-to-weight ratio is the ratio of instantaneous thrust of rocket and jet engines to aircraft or rocket weight.
In other words: the "lift to drag ratio" is a parameter for total aircraft aerodynamics efficiency whereas the "thrust to weight ratio" is an efficiency factor for total aircraft propulsion.
Topics of Interest
In aerodynamics, the lift-to-drag ratio, or L/D ratio ("ell-over-dee" in the US, "ell-dee" in the UK), is the amount of lift generated by a wing or vehicle, compared to the drag it creates by moving through the air. A "better" L/D ratio is one of the major goals in wing design, since a particular aircraft's needed lift doesn't change, delivering that lift with lower drag leads directly to better fuel economy, climb performance and gliding ratio.
The term is calculated for any particular speed by measuring the lift generated, then dividing by the drag it causes. These vary with speed, so the results are typically plotted on a 2D graph. In almost all cases the graph forms a U-shape, due to the two main components of drag on the wing.
Induced drag is caused by the generation of lift by the wing. Lift generated by a wing is perpendicular to the wing, but since wings typically fly at some small angle of attack, this means that a component of the force is directed to the rear. The rearward component of this force is seen as drag. At low speeds an aircraft has to generate lift with a higher angle of attack, thereby leading to greater induced drag. This term dominates the low-speed side of the L/D graph, the left side of the U.
Profile drag is caused by air hitting the wing itself. This form of drag, simply another name for wind resistance, varies with the square of speed (see drag equation). For this reason profile drag is only a real factor at higher speeds, forming the right side of the L/D graph's U shape. Profile drag is lowered primarily by using thinner wings, but such a shape often leads to less low-speed lift, and thus higher induced drag.
It is the bottom point of the graph, the point where the combined drag is at its lowest, that the wing is performing at its best. For this reason designers will typically select a wing with its L/D peak at the chosen cruising speed of the aircraft, thereby maximizing economy. Like all things in aeronautical engineering, the lift-to-drag ratio is not the only consideration for wing design. Performance at high angle of attack and a gentle stall are often considered more important, and for this reason easy-to-fly wing designs like the Clark-Y continue to be used even though many more efficient wings have since been designed.
Gliding ratio: As the aircraft fuselage and control surfaces will also add drag and possibly some lift, it is fair to consider the L/D of the aircraft as a whole. As it turns out, the gliding ratio, which is the ratio of an (unpowered) aircraft's descent to its forward motion, is numerically equal to the aircraft's L/D. This is especially of interest in the design and operation of high performance gliders (called sailplanes), which can have gliding ratios approaching 60 to 1 (60 units of distance forward for each unit of descent) in the best cases, but with 30:1 being considered good performance for general recreational use. Achieving a sailplane's best L/D in practice requires precise control of airspeed and smooth and restrained operation of the controls to reduce drag from deflected control surfaces. In zero wind conditions, L/D will equal altitude lost divided by distance traveled. Achieving the maximum distance for altitude lost in wind conditions requires further modification of the best airspeed, as does alternating cruising and thermaling. To achieve high speed across country, gliders are often loaded with water ballast to increase the airspeed (allowing better penetration against a headwind). As noted below, to first order the L/D is not dependent on speed, although the faster speed means the airplane will fly at higher Reynold's number.
For maximum range, one should fly at the point on the graph with minimum drag. Since the lift on an aircraft must equal the weight, this point is equal to the maximum L/D point. (The speed should decrease a bit during the flight because the optimal speed decreases as the plane uses up fuel and becomes lighter.) Because this theoretical speed may still be slightly exceeded without significant losses in efficiency, the "long range cruise speed" is normally slightly higher than the maximum range speed. There is a trade-off between saving fuel and saving time. The upper limit of speed is dictated by available (continuous) thrust and is not shown on the graph.
Supersonic/hypersonic lift to drag ratios: At very high speeds, lift to drag ratios tend to be lower. Concorde had a lift/drag ratio of around 7 at Mach 2, whereas a 747 is around 17 at about mach 0.85.
Thrust-to-weight ratio is, as its name suggests, the ratio of instantaneous thrust to weight (where weight means weight at the Earth’s surface). It is a dimensionless parameter characteristic of rockets and jet engines, and of vehicles propelled by such engines (typically space launch vehicles and jet aircraft). It is used as a figure of merit for quantitative comparison of engine or vehicle design.
The value is larger for an engine than for a whole launch vehicle; the engine thrust-weight is of use since it determines the maximum acceleration that any vehicle using that engine could theoretically achieve with minimum propellant and structure attached.
For a takeoff using pure thrust and no wings, the thrust-weight ratio for the vehicle has to be more than one (for launch from the Earth's surface, for launch from the Moon it only needs to be more than 0.1654). In general, the thrust-to-weight ratio is numerically equal to the g-force that the vehicle can pull, provided the g-force exceeds local gravity then takeoff can occur.
Many factors affect a thrust-to-weight ratio, and it typically varies slightly over the flight. For valid comparison, thrust should be measured under controlled conditions. The main factors that affect thrust include freestream air temperature, pressure, density, and composition. Depending on the engine or vehicle under consideration, the actual performance will often be affected by progressive fuel consumption (causing a rise in thrust-weight ratio), buoyancy, and local gravitational field strength.
Example: The Russian-made RD-180 rocket engine (which powers Lockheed Martin’s Atlas V) produces 3,820 kN of sea-level thrust and has a dry mass of 5,307 kg. Using the Earth surface gravitational field strength of 9.80665 m/s², the sea-level thrust-to-weight ratio is computed as follows: (1 kN = 1000 N = 1000 kg⋅m/s²)
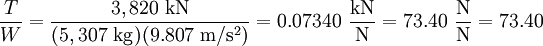
Source: Wikipedia (All text is available under the terms of the GNU Free Documentation License and Creative Commons Attribution-ShareAlike License.)
|



